Python_(herschelhelp_internal)

xxxxxxxxxxMaster catalogue used: __master_catalogue_elais-n1_20171016.fits__<br>Number of rows: 4,026,292<br>Surveys included:<br>| Survey | Telescope / Instrument | Filters (detection band in bold) | Location ||-----------|-----------------------------|:------------------------------------------:|-----------------------------|| SpARCS | CFHT / MegaCam | ugrz | dmu0_SpARCS || INT / WFC | Isaac Newton Telescope / Wide Field Camera | ugriz | dmu0_INTWFC || PS1 3PSS | Pan-STARRS1 / Pan-STARRS1 | g**r**izy | dmu0_PanSTARRS1-3SS || HSC-SSP | Hyper Suprime | grizy | dmu0_HSC-SSP || UKIDSS / DXS | UKIRT / WFCAM | JK | dmu0_UKIDSS-DXS || SWIRE | Spitzer / IRAC | **IRAC1**,**IRAC2**,**IRAC3**,**IRAC4** | dmu0_DataFusion-Spitzer || SERVS | Spitzer / IRAC | **IRAC1**, **IRAC2** | dmu0_DataFusion-Spitzer |Master catalogue used: master_catalogue_elais-n1_20171016.fits
Number of rows: 4,026,292
Surveys included:
| Survey | Telescope / Instrument | Filters (detection band in bold) | Location |
|---|---|---|---|
| SpARCS | CFHT / MegaCam | ugrz | dmu0_SpARCS |
| INT / WFC | Isaac Newton Telescope / Wide Field Camera | ugriz | dmu0_INTWFC |
| PS1 3PSS | Pan-STARRS1 / Pan-STARRS1 | grizy | dmu0_PanSTARRS1-3SS |
| HSC-SSP | Hyper Suprime | grizy | dmu0_HSC-SSP |
| UKIDSS / DXS | UKIRT / WFCAM | JK | dmu0_UKIDSS-DXS |
| SWIRE | Spitzer / IRAC | IRAC1,IRAC2,IRAC3,IRAC4 | dmu0_DataFusion-Spitzer |
| SERVS | Spitzer / IRAC | IRAC1, IRAC2 | dmu0_DataFusion-Spitzer |
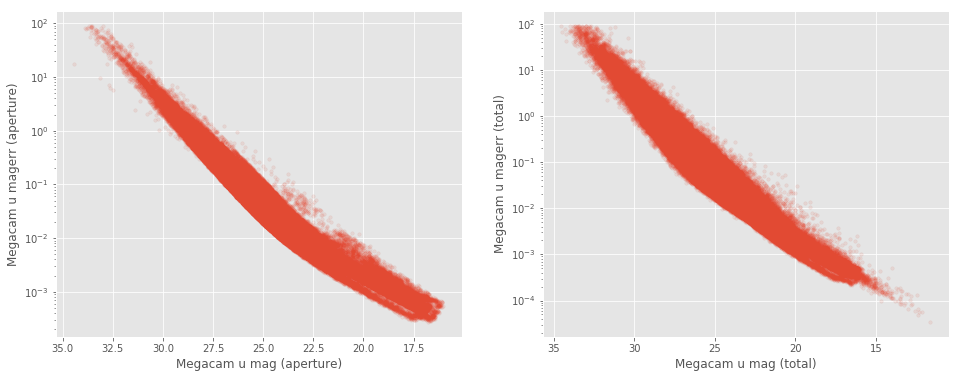
xxxxxxxxxxAt faint magnitudes (mag > 24), some surveys have very large errors on the magnitude. These objects may be unreliable for science puposes.<br>This includes __HSC-SSP aperture and total__ (at mag > 24) for which magnitudes can be as faint as 60mag (!!) with errors up to 10$^{13}$, __CFHT aperture and total__ magnitudes (at mag > 22) and __IRAC1, IRAC2 aperture and total__ magnitudes (at mag > 18). <br>Also, for __INT aperture and total__ magnitudes (at mag > 22) and __UKIDSS aperture and total__ magnitudes (at m > 27) very few sources also have very large errors.<br><img src="help_plots/ELAIS-N1_magVSmagerr_Megacam_u_mag_total.png" />At
faint magnitudes (mag > 24), some surveys have very large errors on
the magnitude. These objects may be unreliable for science puposes.
This includes HSC-SSP aperture and total (at mag > 24) for which magnitudes can be as faint as 60mag (!!) with errors up to 10, CFHT aperture and total magnitudes (at mag > 22) and IRAC1, IRAC2 aperture and total magnitudes (at mag > 18).
Also, for INT aperture and total magnitudes (at mag > 22) and UKIDSS aperture and total magnitudes (at m > 27) very few sources also have very large errors.
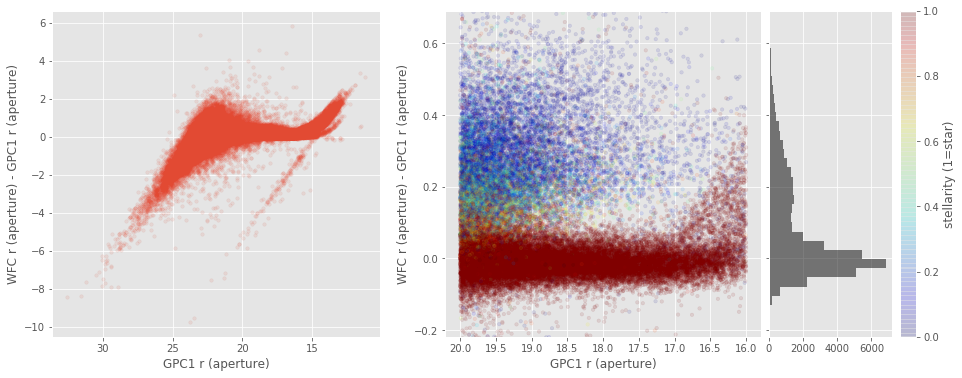
xxxxxxxxxxIn most of the case when comparing the aperture magnitudes between surveys, we observed a two peak distribution in the difference between the magnitudes ($\Delta_{mag} = mag_{survey1} - mag_{survey2}$). We have one peak around 0 for point-source objects, with a small spread. And a second peak at higher $\Delta_{mag}$ with a larger spread for extended objects; implying a different aperture correction between surveys for these objects.<br>That means that galaxies will not have the same aperture magnitude in different surveys. <br>In the griz bands, for bright sources, there is a two peaks distribution when comparing CHFT, INT, Pan-STARRS, and HSC-SSP aperture magnitues. Except when comparing HSC-SSP and CFHT magnitudes, $\Delta_{mag}$ is similar for point-sources and extended objects.<br><img src="help_plots/ELAIS-N1_apcorrIssues_WFC_r_aperture_-_GPC1_r_aperture.png" />In
most of the case when comparing the aperture magnitudes between
surveys, we observed a two peak distribution in the difference between
the magnitudes (). We have one peak around 0 for point-source objects, with a small spread. And a second peak at higher with a larger spread for extended objects; implying a different aperture correction between surveys for these objects.
That means that galaxies will not have the same aperture magnitude in different surveys.
In the griz bands, for bright sources, there is a two peaks
distribution when comparing CHFT, INT, Pan-STARRS, and HSC-SSP aperture
magnitues. Except when comparing HSC-SSP and CFHT magnitudes, is similar for point-sources and extended objects.
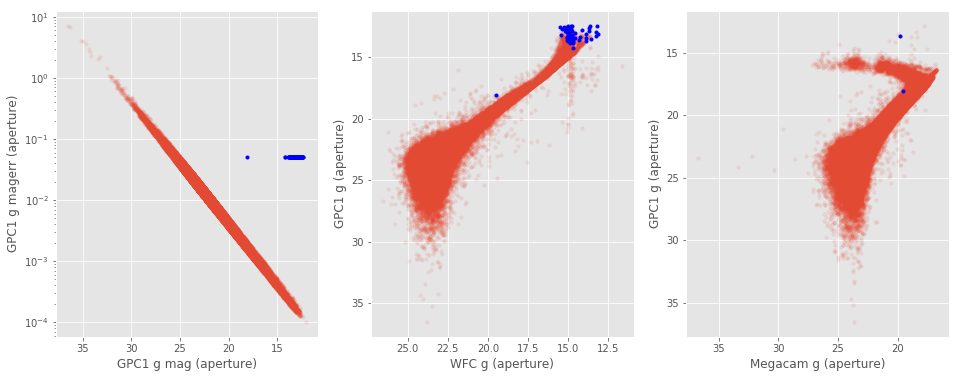
### II.a. Pan-STARRS aperture magnitudeFew Pan-STARRS sources have exactly the same error (of <font color='blue'>0.05000000074505806</font>) on the __aperture and total__ magnitudes in all the grizy bands. The corresponding aperture magnitude should not be trusted for these objects.<br><img src="help_plots/ELAIS-N1_gpc1Issues_GPC1_g_mag_aperture.png" />Few Pan-STARRS sources have exactly the same error (of 0.05000000074505806) on the aperture and total magnitudes in all the grizy bands. The corresponding aperture magnitude should not be trusted for these objects.
x
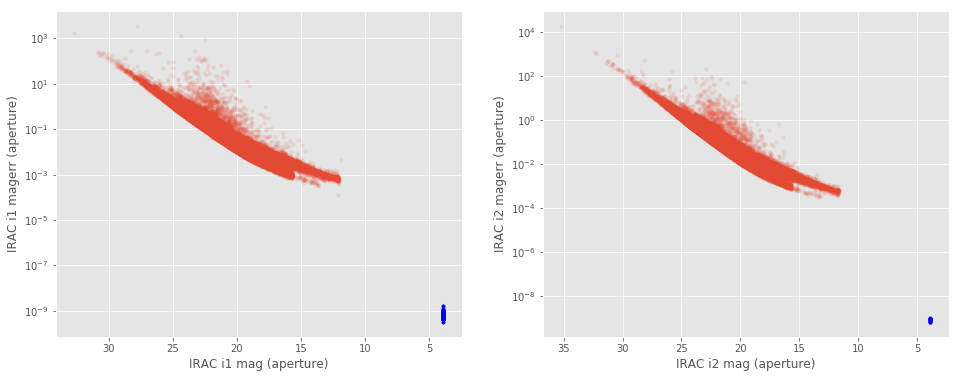
### II.c IRAC aperture magnitudeFew IRAC sources have exactly the same aperture magnitude (of <font color='blue'>3.9000000001085695</font>) in the IRAC1 and IRAC2 bands. These magnitudes also have extremely small errors (around 10$^{-8}$-10$^{-9}$). The corresponding magnitudes should not be trusted. <br><img src="help_plots/ELAIS-N1_iracIssues_i1_i2.png" />Few IRAC sources have exactly the same aperture magnitude (of 3.9000000001085695) in the IRAC1 and IRAC2 bands. These magnitudes also have extremely small errors (around 10-10). The corresponding magnitudes should not be trusted.
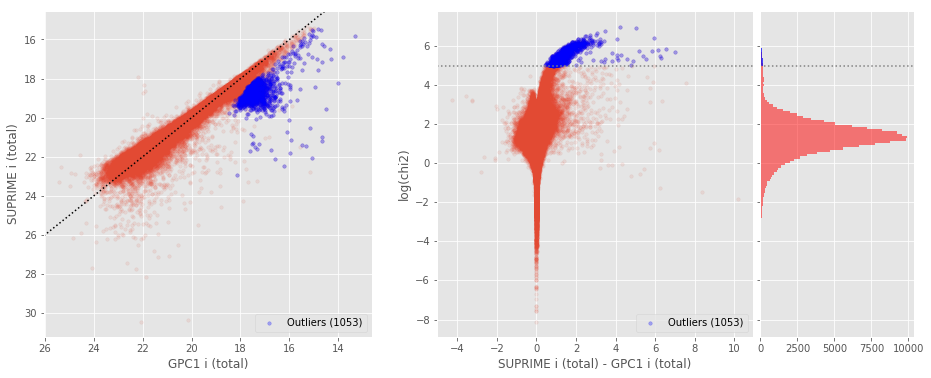
xxxxxxxxxx### II.b. OutliersBy comparing magnitude in the same band between different surveys, we can see that some magnitudes are significanlty different could not be trusted. <br>The outliers are identified to have a large weighted magnitude difference (equivalent of the $chi^2$).$$chi^2 = \frac{(mag_{1}-mag_{2})^2}{magerr_{1}^2 + magerr_{2}^2}$$ <br>We used the 75th and 25th percentile to flagged the objects 5$\sigma$ away on the large values tail of the $chi^2$ ditribution. (__NB:__ bright sources tend to have their errors underestimated with values as low as $10^{-6}$, which is unrealistic. So to avoid high $chi^2$ due to unrealistic small errors, we clip the error to get a minimum value of 0.1% (i.e. all errors smaller then $10^{-3}$ are set to $10^{-3}$).)<br><br>$$outliers == [chi^2 > (75th \;percentile + 3.2\times (75th \;percentile - 25th \;percentile))]$$<img src="help_plots/ELAIS-N1_outliers_SUPRIME_i_total_-_GPC1_i_total.png"/>By comparing magnitude in the same band between different surveys, we
can see that some magnitudes are significanlty different could not be
trusted.
The outliers are identified to have a large weighted magnitude difference (equivalent of the ).